デジタル推進課

KNIME・Excel Macro・Power Automateなど日々の業務で使用できる自動化ツールを中心に書き綴ります

KNIME - 時系列解析の第一歩！株価の移動平均を求めるには？ ~Moving Average~

KNIME KNIME - 中級編 Node紹介

f:id:makkynm:20210512175315p:plain

はじめに
覚えてほしいこと
やりたいこと
Moving Averageの使い方
ちょっと一言
- 様々な移動平均の手法
- その他のNodeのConfiguration
おわりに
KNIMEに関する本
参考リンク

はじめに

こんにちは、自動化大好きまっきーです。突然ですが、移動平均ってご存知ですか？

分析の基礎のきみたいなものだと思います。

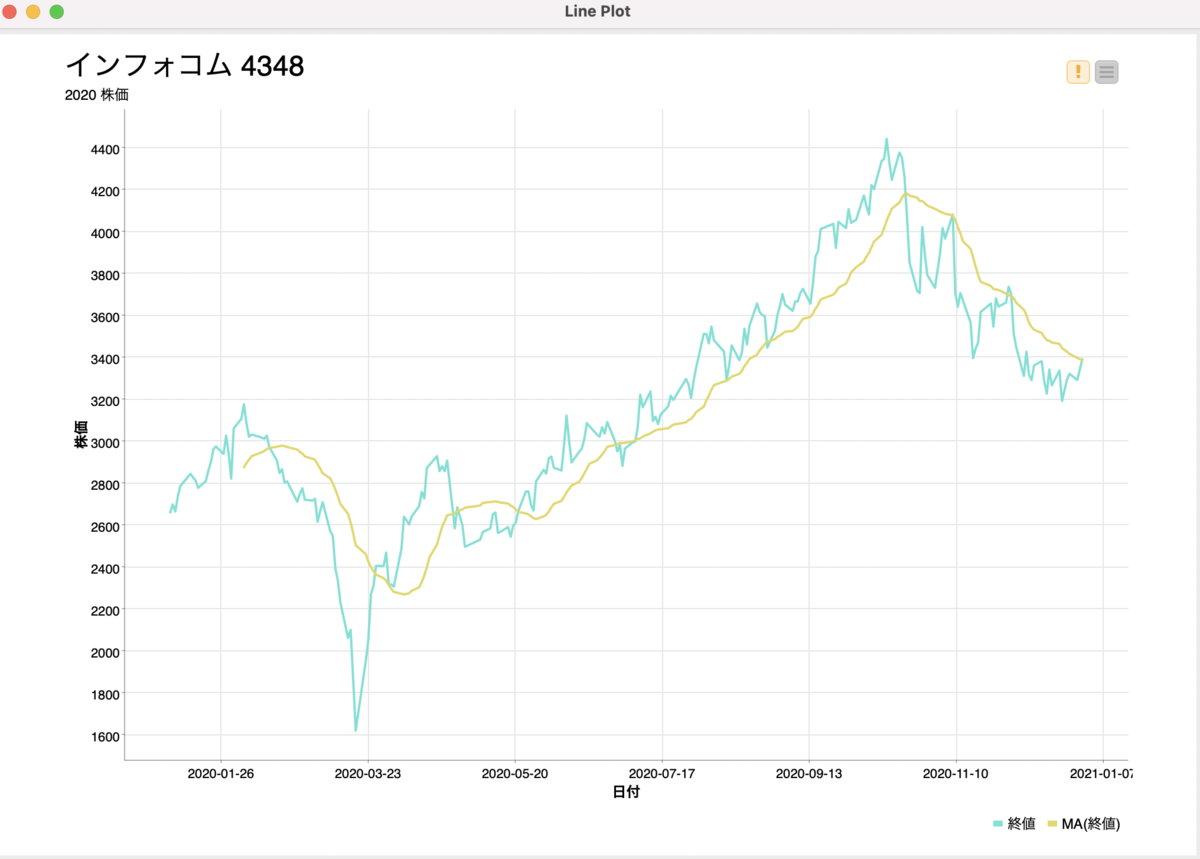
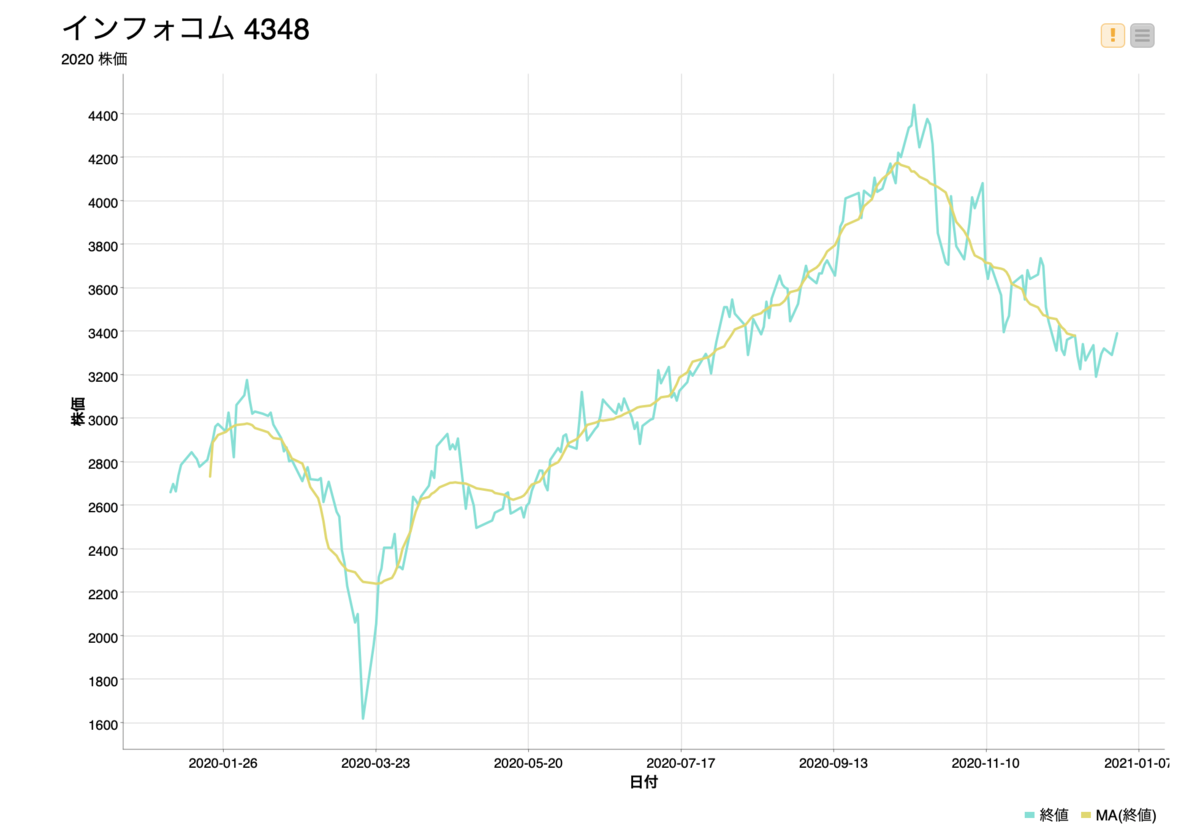
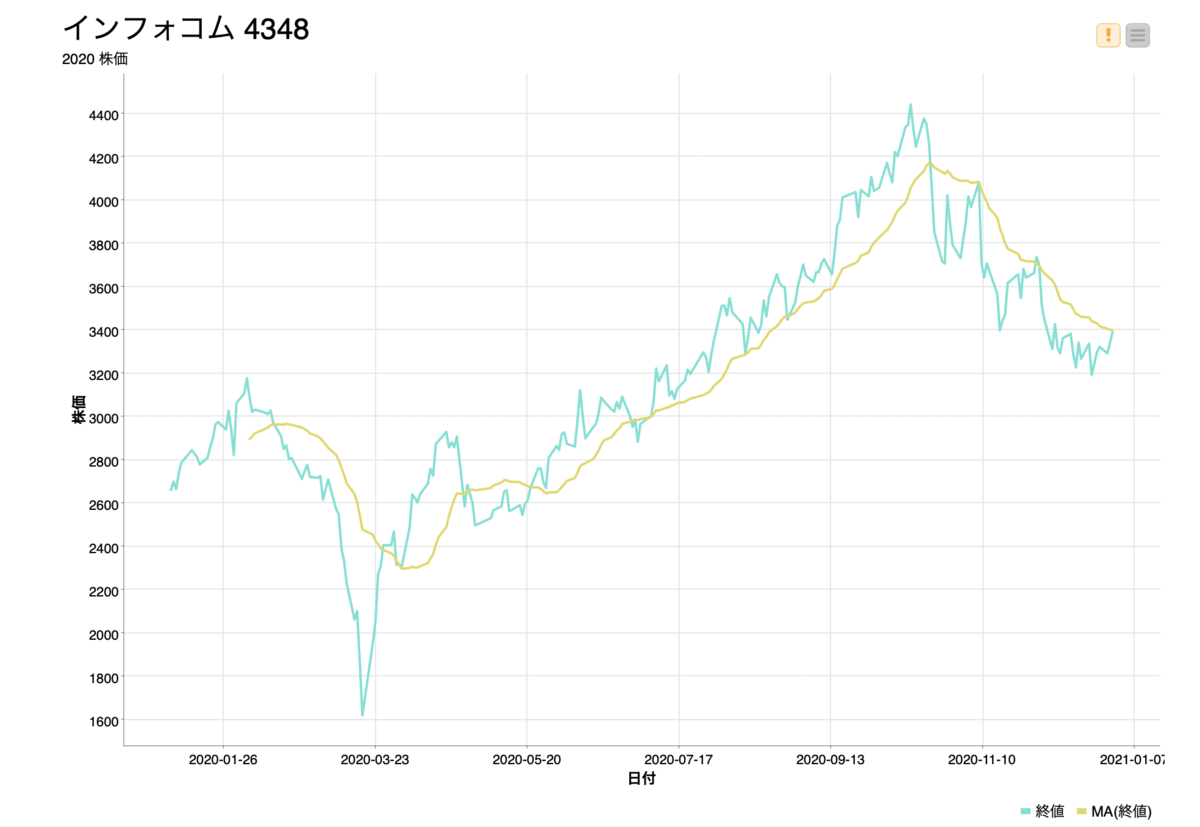
よく分からないなーという人、株価のグラフで見たことないですか？移動平均を使えば、日々日々の変化ではなくある一定の期間で平均を取るので、現在上がり基調なのか下がり基調なのかが分かります。

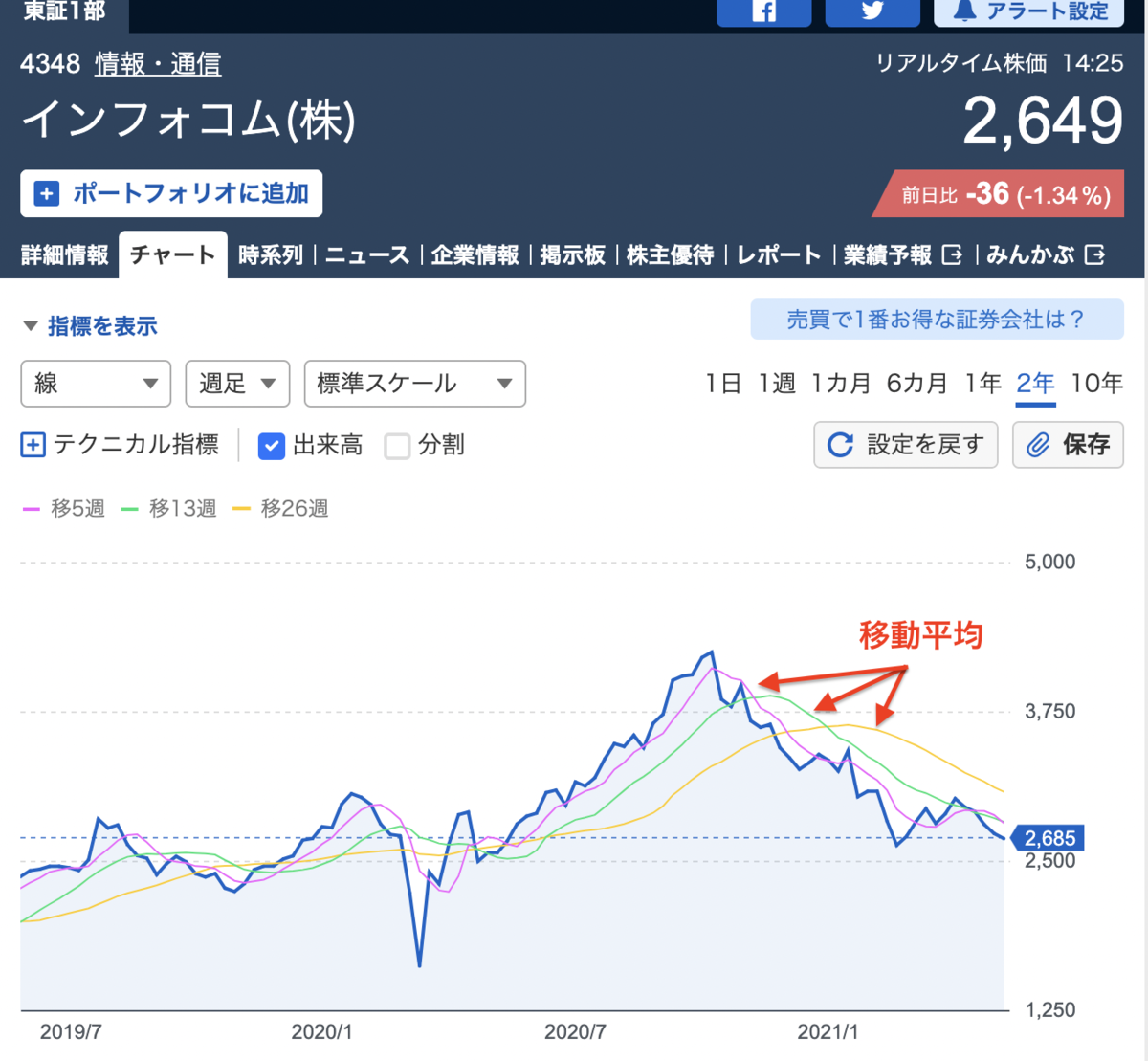
f:id:makkynm:20210512142708p:plain — 移動平均とは？

引用：インフォコム(株)【4348】：チャート - Yahoo!ファイナンス

今回はその移動平均をKNIMEで出力する方法について解説したいと思います。Excelでやるとちょっと面倒なんですが、KNIMEだと非常に簡単です。

今回のテーマ ~Moving Average~

f:id:makkynm:20210512143216p:plain — Workflow - Moving Average

覚えてほしいこと

移動平均を使えば時系列データの傾向が簡単に掴める

やりたいこと

今回は例として、KNIMEの日本語サポートをされているインフォコムさん（4348）の2020年の株価（終値）を前後10日、21日間の移動平均を求めて同じグラフに出力してみたいと思います。

f:id:makkynm:20210512142943p:plain — やりたいこと - 株価の移動平均

元データは下記のサイトからcsvでダウンロードさせていただきました。

4348 インフォコム(株) 2020年度の株価データ・株価データ、CSVダウンロード | 株式投資メモ・株価データベース

f:id:makkynm:20210512143141p:plain — 元データをcsvでダウンロード

Moving Averageの使い方

移動平均を簡単に求めることができるNodeです。時系列データの移動平均を取る場合、時系列ごとに行がSortされていることが前提となります。参考：Sorter

設定は簡単なのですが、移動平均の種類がたくさんあるので自分にあった移動平均の手法を選びましょう。

Workflow - Moving Average

f:id:makkynm:20210512143216p:plain — Workflow - Moving Average

workflowは下記からダウンロードできます。

Confirm - Before After

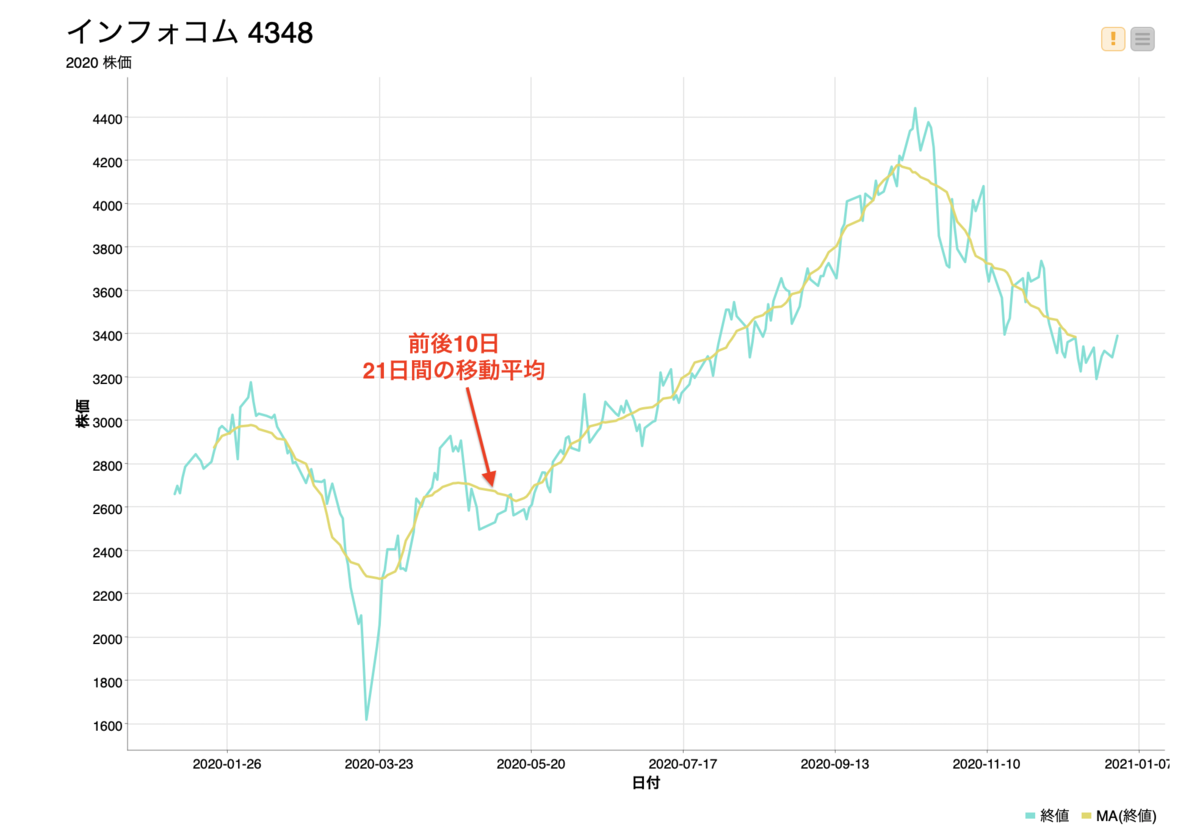
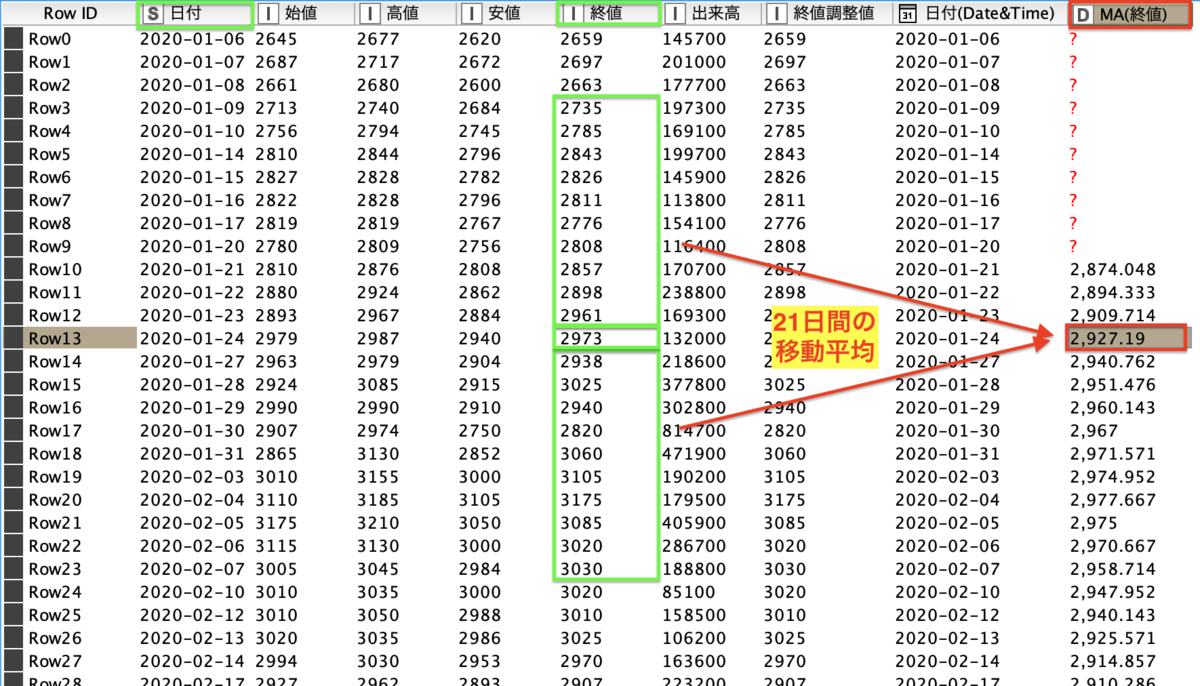
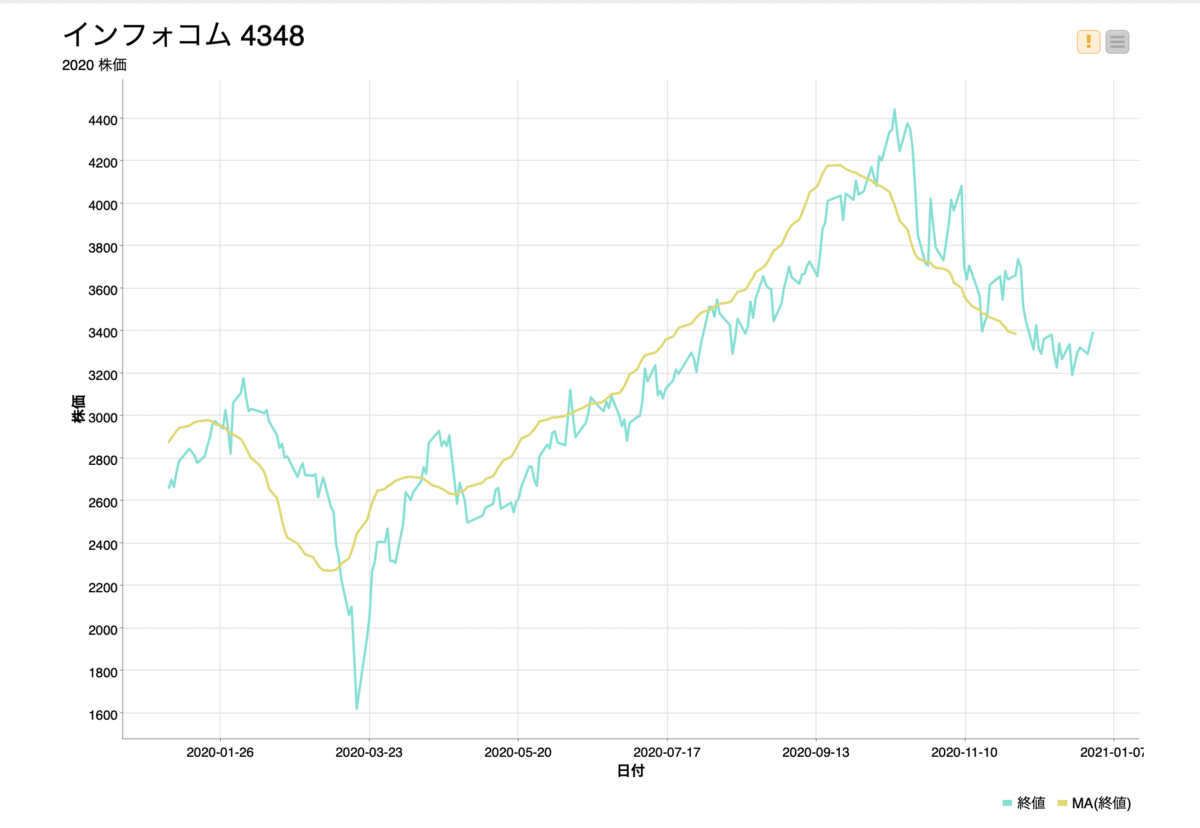
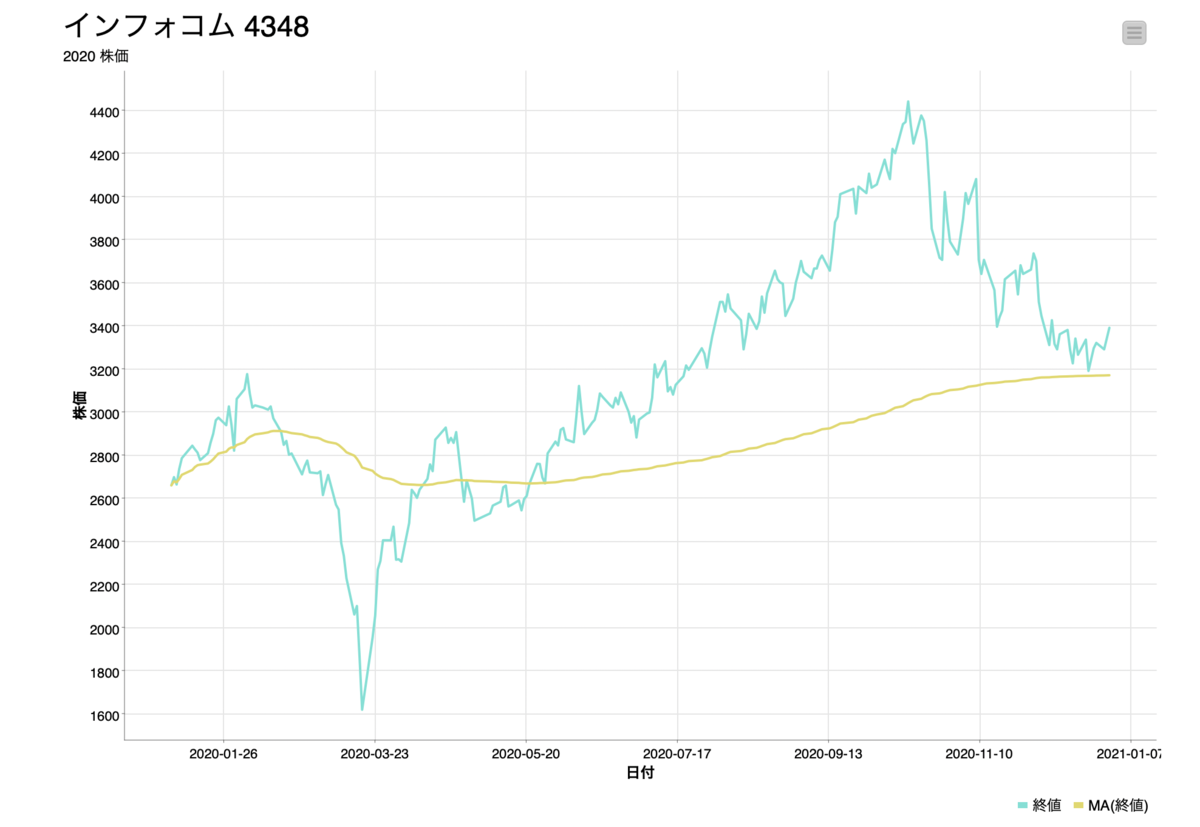
前後10日、21日間の移動平均とはどういうことか、こちらのOutputを見ていただければわかるのではないでしょうか。21行の固定枠を持っていて、その平均をずらしながら取っていく方法です。

最初の10行は平均を取る十分な数字がないので欠損値になっています。

また、コラムの名前は、MA(コラム名)という形で命名されます。

f:id:makkynm:20210512144204p:plain — Confirm - Moving Average

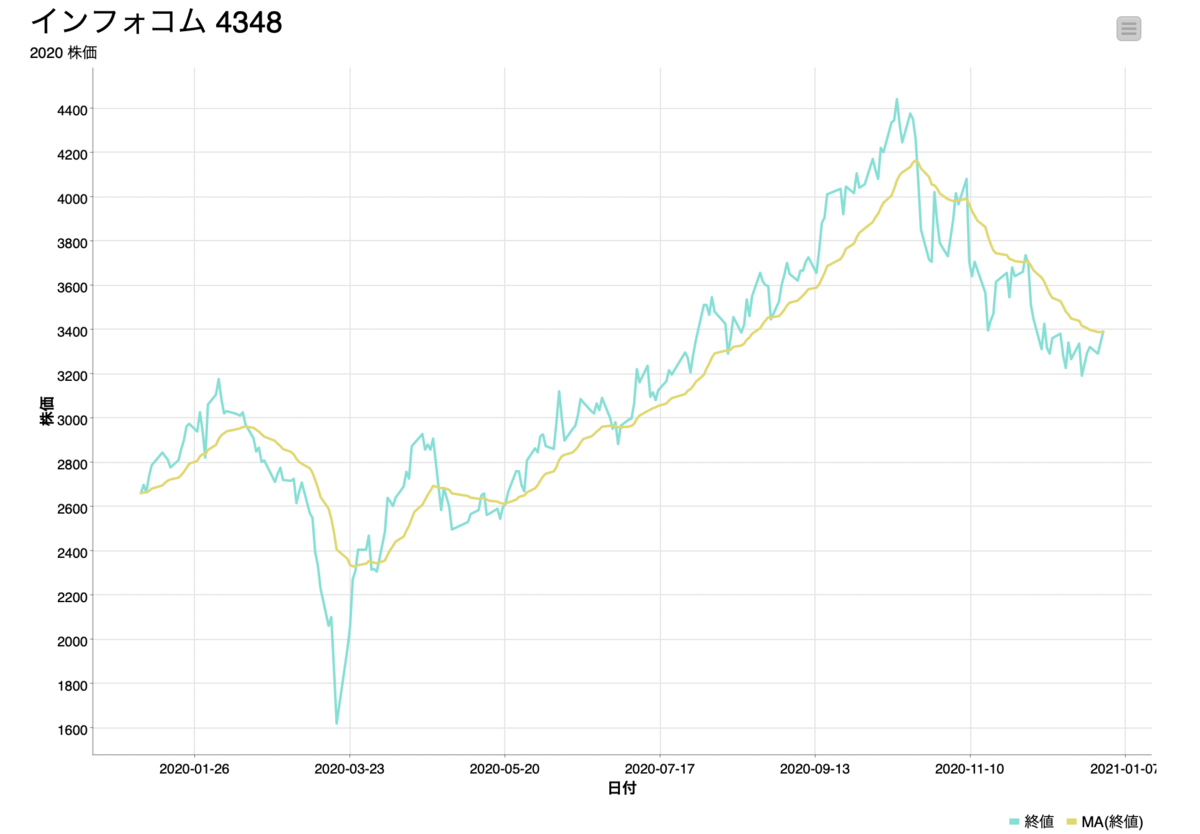
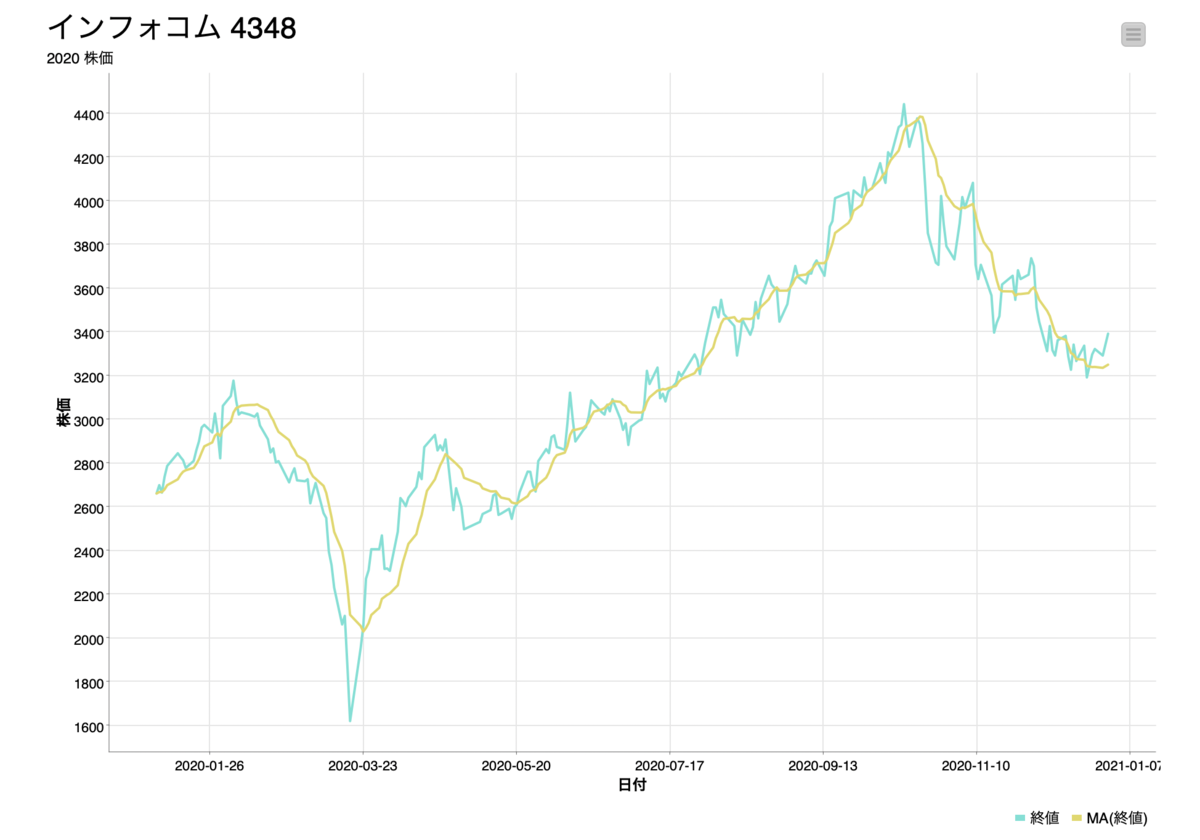
線グラフで表すと下図のようになっており、日々のデータが移動平均を取ることによって滑らかになっていることが分かります。

f:id:makkynm:20210512142943p:plain — Confirm - Moving Average（線グラフ）

Configure - Moving Average

Configureですが、非常に分かりやすいと思います。

f:id:makkynm:20210512145013p:plain — Configure - Moving Average

Step1 - 移動平均の取り方の選択

まずは移動平均の種類と枠の大きさを選択します。

Type of Moving Average :移動平均の種類（今回は最も単純なCenter simpleという前後同じだけの数を取る方法を指定）
Window Length: 移動平均の枠の大きさ（今回は前後10日なので21行分）

注意点として、移動平均の種類によって、Window Lengthの指定できる数が変わります。例えば、今回指定した中央を基準として前後同じだけの数を取る方法の場合、奇数のみしか指定できません。

Step2 - 対象コラム選択

Remove original columns にチェックを入れると、移動平均を計算する元としたコラムをOutputで削除します。

次に対象コラムの選択です。移動平均を求めたいコラムをIncludeの方に持っていきます。Outputのコラム名はMA(元コラム名)となります。

ちょっと一言

様々な移動平均の手法

先ほどは最も簡単な移動平均の方法を使用しましたが、KNIMEは解析ツールなので様々な移動平均の方法が選択できます。

k: Window length 枠の大きさ

n: 移動平均を求める行番号

とりあえずNode Pitの数式に基づいて書きましたが、これ違くないか？というのもあったので、ふーんくらいに受け取ってください。久々にTex使ったので数式少し汚いかもです。。Tex書くの疲れた。。

Backward simple - 前方単純移動平均

移動平均の枠を前に取った形です。

kをwindow length、v(i)を計算元コラムの値とするとき、

n番目の移動平均 = n-(k-1) 番目からn番目の数値の平均
$MA(n) =\frac{1}{k}\cdot\sum_{i=n-(k-1)}^{n}{v_i}$

f:id:makkynm:20210512161902p:plain — Backward simple k=21

Center simple - 中心単純移動平均

移動平均の枠を真ん中に取った形です。

kをwindow length、v(i)を計算元コラムの値とするとき、

n番目の移動平均 = n-(k-1) 番目からn番目の数値の平均

$MA(n) =\frac{1}{k}\cdot\sum_{i=n-\frac{n-1}{2}}^{n+\frac{n-1}{2}}{v_i}$

f:id:makkynm:20210512142943p:plain — Center simple

Forward simple - 後方単純移動平均

移動平均の枠を後ろに取った形です。

n番目の移動平均 = n番目からn+(k-1) 番目の数値の平均

$MA(n) =\frac{1}{k}\cdot\sum_{i=n}^{n+(k-1)}{v_i}$

f:id:makkynm:20210512174310p:plain — Forward simple - 後方単純移動平均

Backward Gaussian - 前方ガウス関数 移動平均

枠を前方に取った時、正規分布で重み付けを行いながら移動平均を取った場合

ガウス関数というのを聞いたことがあるでしょうか。枠内で平均を取るときに正規分布に基づいて重み付けを行なっていき平均を取っていきます。

下記の式あっているか怪しいので、間違っていたら指摘してください。。

通常であれば $\sigma$ は標準偏差、 $\mu$ は平均です。

$MA(n) =\sum_{i=0}^{k-1} Gauss\left( i, k-1,\sigma \right)\cdot v_{n-i}$

$\sigma=\frac{k-1}{4}$

$Gauss\left( i,\mu ,\sigma \right)=\exp{　\frac{-0.5\cdot \left( i -\mu \right) \cdot \left( i -\mu \right) }{\sigma^2}}$

f:id:makkynm:20210512174341p:plain — Backward Gaussian - 前方ガウス関数移動平均

Center Gaussian - 中央ガウス関数 移動平均

枠を中央に取った時、正規分布で重み付けを行いながら移動平均を取った場合

$MA(n) =\sum_{i=0}^{k-1} Gauss\left( i, \frac{k-1}{2},\sigma \right)\cdot v_{n+\left(i-\frac{k-1}{2}\right)}$

f:id:makkynm:20210512174425p:plain — Center Gaussian - 中央ガウス関数移動平均

Forward Gaussian - 後方ガウス関数 移動平均

枠を後方に取った時、正規分布で重み付けを行いながら移動平均を取った場合

$MA(n) =\sum_{i=0}^{k-1} Gauss\left( i, 0,\sigma \right)\cdot v_{n+i}$

f:id:makkynm:20210512174452p:plain — Forward Gaussian - 後方ガウス関数移動平均

Harmonic Mean Center - 中央調和移動平均

調和平均とは、全ての値で逆数を取って求める平均で、元の値が正であることが必要条件となります。

$MA(n) =\left. n \right/ \sum_{i=0}^{k-1} \frac{1}{v_\left(n+\frac{i-\left(k-1\right)}{2}\right)}$

f:id:makkynm:20210512174520p:plain — Harmonic Mean Center - 中央調和移動平均

Cumulative simple - 累積平均

累積しながら平均を取っていくパターンです。

$MA(n) =\frac{1}{n}\cdot\sum_{i=0}^{n-1}{v_i}$

f:id:makkynm:20210512174556p:plain — Cumulative simple - 累積平均

Simple exponential - 指数平滑移動平均

指数平滑移動平均というもので、直近の値より反映するように移動平均を取ったものです。

$MA(0) = v_0$

$EMA(v,n) = MA(n) = \alpha \cdot v_n + (1-\alpha) \cdot MA(n-1)$

$\alpha = \frac{2}{k+1}$

株価の場合の見方の参考：

単純、加重、指数平滑･･･３種類の「移動平均線」の特徴 | 富裕層向け資産防衛メディア | 幻冬舎ゴールドオンライン

直近の価格を2倍にして計算したものです。 5日EMAの場合、5日目の価格を2倍にして合計し、5で割ったものです。そのため、単純移動平均や加重移動平均線と比べて、より直近の価格に重点を置いたものになっています。

f:id:makkynm:20210512174630p:plain — Simple exponential - 指数平滑移動平均

Double exponential - 2重指数平滑移動平均

$MA(n) = 2 \cdot EMA(v,n) - EMA(EMA(v,n),n)$

f:id:makkynm:20210512174656p:plain — Double exponential - 2重指数平滑移動平均

Triple exponential - 3重指数平滑移動平均

$MA(n) = 3 \cdot EMA(v,n) - 3 \cdot EMA(EMA(v,n),n) + EMA(EMA(EMA(v,n),n),n)$

f:id:makkynm:20210512174721p:plain — Triple exponential - 3重指数平滑移動平均

Old Exponential - 旧指数平滑移動平均

$MA(n) = \alpha \cdot v_n + (1-\alpha) \cdot MABackwardSimple(n-1)$

f:id:makkynm:20210512174748p:plain — Old Exponential - 旧指数平滑移動平均

その他のNodeのConfiguration

Node1 - CSV Reader

株価の元データ(csv ファイル)を読み込むNodeです。

新しいCSV Readerになったので、少し以前のVersionと画面は異なるかもしれませんが、基本は同じです。

注意点は、１行目は読み込まない設定にすること、EncodingはShift-JISである部分ですね。

degitalization.hatenablog.jp

f:id:makkynm:20210512150256p:plain — Node1 - csv reader

f:id:makkynm:20210512150316p:plain — Node1 - csv reader

f:id:makkynm:20210512150328p:plain — Node1 - csv reader

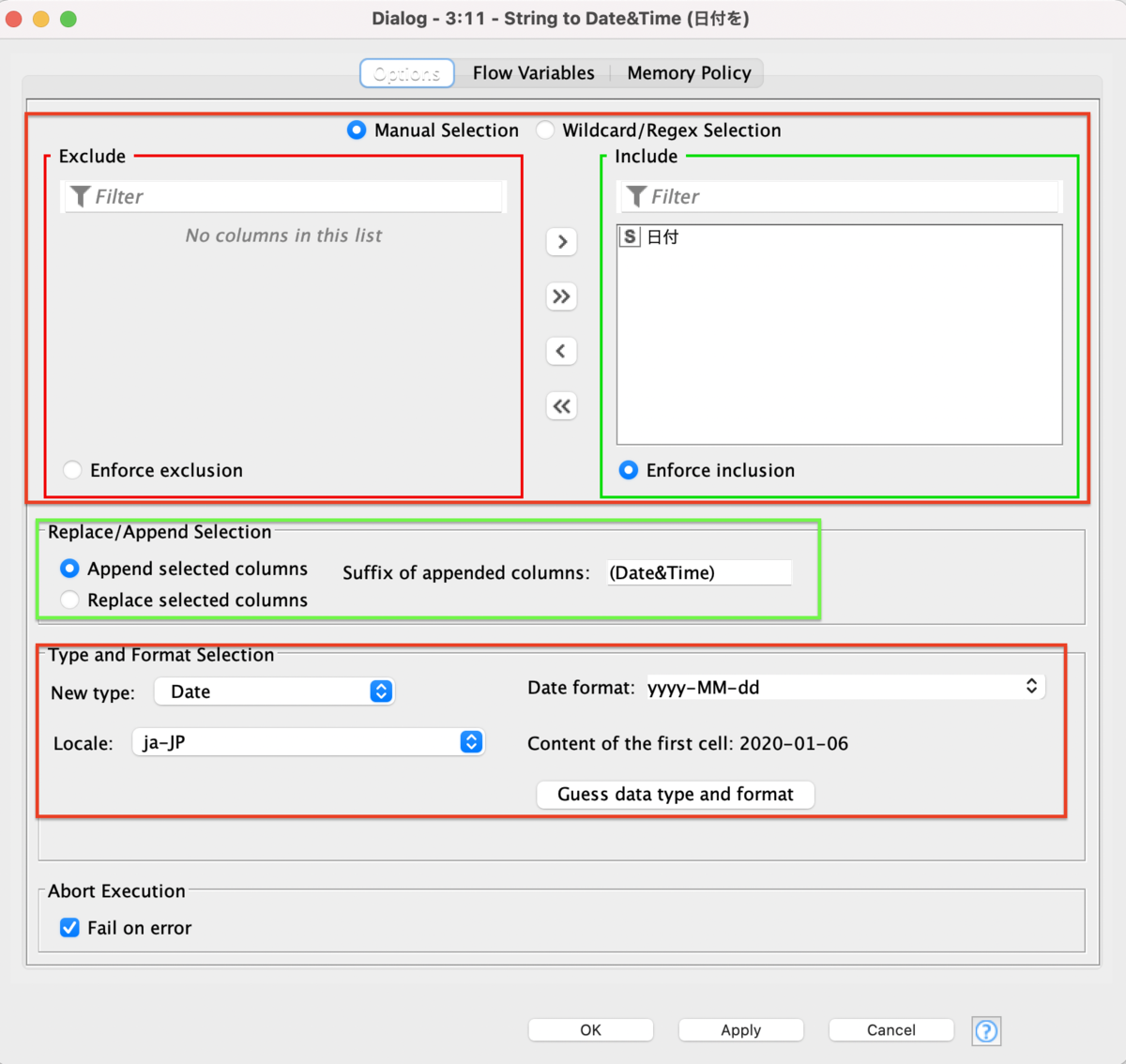
Node2 - String to Date&Time

日付型に変換するNodeです。

degitalization.hatenablog.jp

f:id:makkynm:20210512150624p:plain — Node2 - String to Date&Time

Node 4 - Line Plot

線グラフを作るNodeです。

degitalization.hatenablog.jp

f:id:makkynm:20210512150919p:plain — Node 4 - Line Plot

f:id:makkynm:20210512150932p:plain — Node 4 - Line Plot

f:id:makkynm:20210512150942p:plain — Node 4 - Line Plot

おわりに

お疲れ様でした！KNIMEは解析ツールなので、私が今まで解説してきたのは実はサブの機能に近いです。ただ、今までのNodeの知識は確実に分析を行うための基礎となっていると思います。皆さん機械学習やAIという言葉をきくと私にはできないと思うかもしれませんが、今までのNodeの使い方がマスターできていたら基礎は出来ているので、あとは機械学習用のNodeを追加するだけで出来てしまうんです。

これぞCitizen Developerですね。ぜひマスターしていきましょう。

ではまた！

KNIMEに関する本

KNIMEに関する日本語の本って今これくらいしかないと思うんですよね、、

本がいいなーと言う人はぜひ試してみてください。

AI、IoTを成功に導くデータ前処理の極意

AI、IoTを成功に導くデータ前処理の極意

作者:日立産業制御ソリューションズ
発売日: 2018/09/13
メディア: 単行本

参考リンク

株価情報：
4348 インフォコム(株) 2020年度の株価データ・株価データ、CSVダウンロード | 株式投資メモ・株価データベース

インフォコム(株)【4348】：チャート - Yahoo!ファイナンス
KNIME公式Node Pit（英語）：
Moving Average — NodePit
KNIME Example Workflow（英語）：
Moving Average – KNIME Hub

にほんブログ村